Table of Links
III. TDA Approach to analyzing multiple time series
A. Obtaining point cloud from stock price time-series
B. EE due to the 2008 Financial crisis
C. EE due to COVID-19 pandemic
D. Impact of COVID-19 on different Indian sectors
VII. Acknowledgments and References
II. METHODOLOGY
A. Topological Data Analysis
Topological data analysis (TDA) allows us to extract robust topological features from noisy datasets. One of the advantages of using TDA is its robustness, i.e., the output doesn’t change under small perturbations[29]. In our work, we use Persistent homology which is a powerful tool in TDA, that provides a quantitative representation of how the shape and connectivity of data evolve as the resolution (ε) increases[41].
Sections II A 1– II A 4 contain the definitions and notations from persistent homology used in the paper.
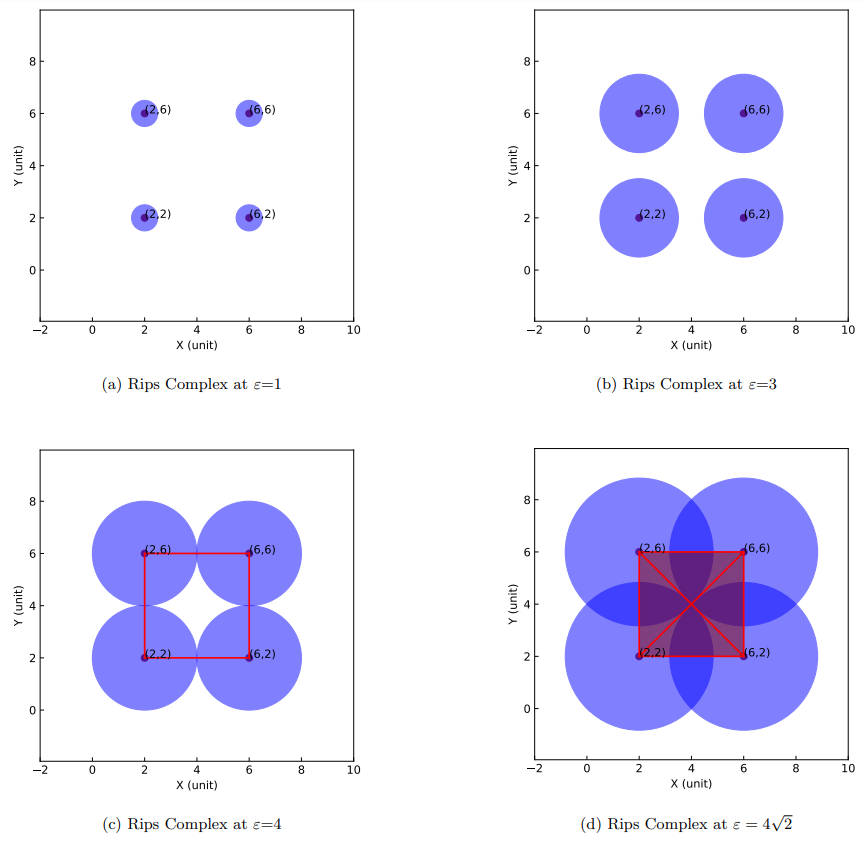
1. Vietoris–Rips Complexes

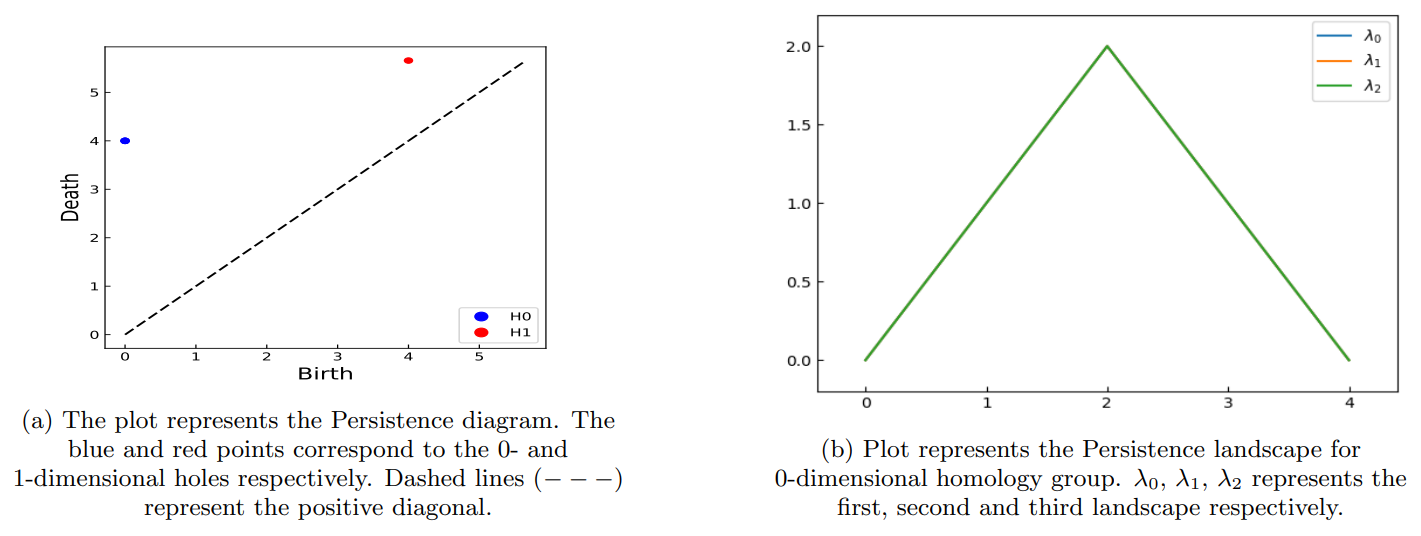
2. Persistence Diagrams

To develop a better understanding of Vietoris–Rips complexes and persistence diagrams through visualization, let us consider the following set of four data points, A = {[2, 2], [2, 6], [6, 2], [6, 6]} in the two-dimensional Euclidean space.

3. Wasserstein Distance

A key advantage of persistence homology is its robustness under small perturbations. If the underlying data changes slightly, the corresponding persistence diagram only moves a small Wasserstein distance from the diagram of the original data[29,44]. This property makes persistence homology a valuable tool for analyzing complex systems.
4. Persistence Landscapes and their Norms

Authors:
(1) Anish Rai, Department of Physics, National Institute of Technology Sikkim, Sikkim, India-737139;
(2) Buddha Nath Sharma, Department of Physics, National Institute of Technology Sikkim, Sikkim, India-737139;
(3) Salam Rabindrajit Luwang, Department of Physics, National Institute of Technology Sikkim, Sikkim, India-737139;
(4) Md.Nurujjaman, Department of Physics, National Institute of Technology Sikkim, Sikkim, India-737139;
(5) Sushovan Majhi, Data Science Program, George Washington University, USA, 20052.
This paper is available on arxiv under CC BY 4.0 DEED license.